带权无向图的连接 矩阵怎么画_带权有向图连接 矩阵0和无穷的区别

1、1起首 在带权无向图的连接 矩阵中，行数和列数分别代表顶点 数和边数，因此必要 先确定图的顶点 数和边数2其次根据顶点 数和边数，初始化一个二维数组作为连接 矩阵，将矩阵中的全部 元素初始化为0或无穷大，表现 没有边毗连 3末了 添补 连接 矩阵，根据图的边权值，将连接 矩阵中的对应元素添补 为实际 的。

2、1先把要讲授 的图在下面展示一下，先看一下2然后在图中的连接 点的值的范围画出连接 表的表头3根据上一步画出的表头分析与其相连的点，这里链表之中背面 有3个框4在链表中第一个框写相连点的顶点 值，第二个框中写权值5根据上述的方式，依次把背面 数字的链表写下来，无向带权图的。

3、连接 矩阵画法如下1先找到一个有向图，有向图和无向图的区别就是多了一些箭头2和无向图刚刚开始雷同 ，都是先找到图内里 值的范围，画出正方形框3然后从0连接 点开始探求 与0相连的连接 点4找到连接 点之后，可以看到每条连线上都有权值，看箭头正向的写连线上的值，反向不通的写正无穷。

4、所要求赋权无向图的连接 矩阵和连接 表，尚有 最小支持 树见下图。

5、5按照上述的方式依次写出1，2，3，4的连接 矩阵履历 步调 1以无向图的例子来举行 讲授 2可以看到这个图的每一个顶点 上都有数字，先看一下这些数字的取值范围，根据范围画出矩形框3从0开始看哪些顶点 和0顶点 相连，把这些相连的顶点 都找出来4然后根据你画的谁人 正方形的边上的数字，看看对应的。

6、空间复杂度方面，连接 矩阵表现 法的存储量是On^2，此中 n为顶点 数创建无向网络的算法起首 必要 输入顶点 数和边数，然后逐个读取顶点 信息和边的毗连 环境 ，末了 添补 连接 矩阵这个过程的时间复杂度为On+n^2+e，此中 e是边的数量 比方 ，图G5和G6的连接 矩阵A1和A2，以及带权图的A3和A4，都是通过。

7、在图的表现 法中，连接 矩阵是一种常用的方法它将顶点 间的相邻关系抽象为矩阵情势 ，通过一个n阶方阵来表现 图G=V，E，此中 n为顶点 数在无向图中，连接 矩阵是对称的，表现 两个顶点 之间是否存在边而在有向图中，矩阵是对角线不对称的，反映了边的方向连接 矩阵的每个元素w ij ，若表现 边的。

8、如图所示点击下图，可查察 大图。

9、留意 到如下四点，就可以写出此图的连接 矩阵1 因这个图有4个结点，故连接 矩阵A为4X4矩阵2 依结点的序号依次分列 ，记为1， 2， 3， 43连接 矩阵的特性 又因这个图是无向图，故A为对称矩阵，以是 A_ij = A_ji 这个特性 可用于验证结果 4 盘算 矩阵元素若结点i与 j相邻，则A_。

10、带权无向图的连接 矩阵是一种表现 图中顶点 之间关系的数据布局 它的特点如下1对称性带权无向图的连接 矩阵是一个对称矩阵，即矩阵的第i行第j列的元素与第j行第i列的元素相称 这是由于 在无向图中，假如 顶点 i与顶点 j之间存在一条边，那么顶点 j与顶点 i之间也肯定 存在一条边2对角线元素为0。

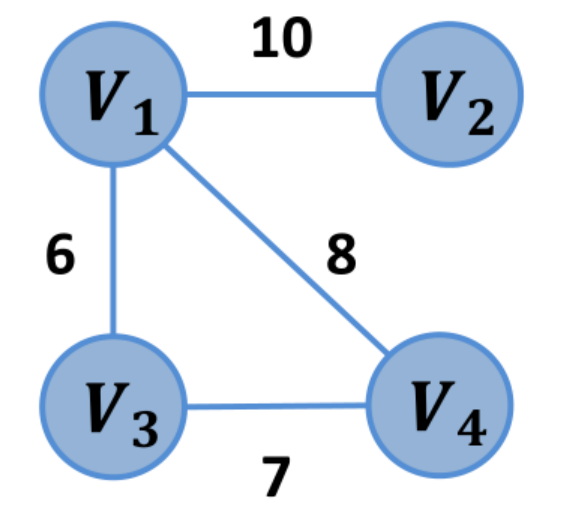
11、连接 表v1 v2 v3 v4 v2 v1 v3 v4 v3 v1 v2 v4 v1 v2 深度遍历序列v1 v2 v3 v4 对应的天生 树包罗 的边是e12， e24， e23 广度遍历序列v1 v2 v4 v3 对应的天生 树包罗 的边是e12， e14， e23。

12、图是一种非常紧张 的数据布局 ，而有向图又是图中一种非常常 用的布局 下面来先容 有向图的连接 矩阵画法工具质料 数位板 Easypaint tool sai 方法步调 1 如下图所示，怎样 根据有向图画出其连接 矩阵2 起首 ，画出矩阵的外围方框，然后在横向和竖向分别按次序 标识出各个连接 点的位置，如下图所示。

13、在无向图中，盘算 顶点 i的度即与其相连的边的数量 只需查察 第i列的全部 元素之和，由于 连接 矩阵的对称性使得这些元素的和相称 对于有向图，顶点 i的出度出边的数量 由第i行的元素之和给出，入度入边的数量 则由第i列的元素之和给出值得留意 的是，由于无向图的连接 矩阵对称且对角线为零。

14、连接 矩阵是表现 图网的结点的连接 关系的方阵，有n个结点的图的连接 矩阵有n行，n列内含n^2个数，假如 只是表现 连接 关系的，用1表现 相邻，用0表现 不相临，连接 方阵由0和1构成 假如 是无向图，其连接 矩阵是对称方阵假如 是有向图，其连接 矩阵黑白 对称方阵假如 是网，矩阵元素表现 权值，大概 是。

15、以是 其连接 矩阵为深度优先搜刮 是指按照深度方向搜刮 ，它雷同 于树的先根遍历深度优先算法的根本 头脑 是若此时图中尚有 顶点 未被访问，则另选图中一个未被访问的顶点 作为起始点，重复上述深度优先搜刮 过程，直至图中全部 顶点 均被访问过为止1访问出发点v02依次以v0的未被访问的连接 点为。

标签：带权无向图的邻接矩阵怎么画连接权无向权有向